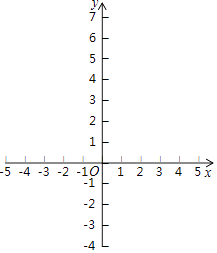题目内容
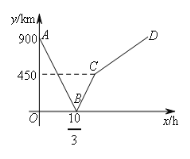
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,各自到达终点后停止行驶。设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,则两车相遇之后又经过___________小时,两车相距720km.
【答案】![]()
【解析】
先求出快车和慢车的车速,根据图形信息确定![]() h两车相遇,第5小时,快车到达终点停止运动,此时两车相距450km,因此只要慢车再走270km辆车就会相距720km.求出慢车所用的总时间与相遇时的时间相减即可.
h两车相遇,第5小时,快车到达终点停止运动,此时两车相距450km,因此只要慢车再走270km辆车就会相距720km.求出慢车所用的总时间与相遇时的时间相减即可.
解:由图可知A(0,900),B(![]() ,0)
,0)
∴直线AB解析式为:y=-270x+900,
由题可知AB与BC的速度不变,
∴设BC段的函数解析式为y=270x+b,
代入B(![]() ,0),得b=-900,
,0),得b=-900,
∴直线BC解析式为:y=270x-900,
∴C(5,450)
∴慢车的速度 450![]() 5=90km/h,
5=90km/h,
快车的速度![]() 90
90![]() (5-
(5-![]() )=180km/h,
)=180km/h,
∴第5小时,快车到达终点停止运动,此时两车相距450km,
∴720![]() 90=8,即第8小时两车相距720km,
90=8,即第8小时两车相距720km,
∴8-![]() ,
,
故答案是![]() .
.

练习册系列答案
相关题目