题目内容
某商业公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的销售和生产进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图1);一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示,其中6月份成本最高(如图2).
(1) 一件商品在3月份出售时的利润是多少元?(利润=售价-成本)
(2)求图2中表示一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30 000件,请你计算一下该公司在一个月内最少获利多少元?
(1) 一件商品在3月份出售时的利润是多少元?(利润=售价-成本)
(2)求图2中表示一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30 000件,请你计算一下该公司在一个月内最少获利多少元?

(1)5元 (2) (3)110000元
(3)110000元
 (3)110000元
(3)110000元试题分析:
解:(1)由图象知:3月份每件商品售价6元,成本1元,故可得,一件商品在3月份出售时的利润为5元.
(2) 由图知,抛物线的顶点为(6,4),故可设抛物线的解析式为Q=
 .
.∵抛物线过(3,1)点,∴a(3-6)2+4=1.解得a=
 .故抛物线的解析式为Q=
.故抛物线的解析式为Q= ,即
,即 ,其中t=3,4,5,6,7.
,其中t=3,4,5,6,7.(3) 设每件商品的售价M(元)与时间t(月)之间的函数关系式为M="k" t+ b.
∵线段经过(3,6)、(6,8)两点,∴M=
 ,其中t=3, 4,5,6,7.
,其中t=3, 4,5,6,7. 故可得:一件商品的利润W(元)与时间t(月)的函数关系式为:W=M-Q=
 ,
, 其中t=3,4,5,6,7.当t=5时,W有最小值为
 元,即30000件商品一个月内售完至少获利30000×
元,即30000件商品一个月内售完至少获利30000× =110000(元).答:该公司一个月内至少获利110000元.
=110000(元).答:该公司一个月内至少获利110000元.点评:该题相对较难,涉及的知识点较多,其中对于函数最值的运用是常考题,学生可通过画图协助分析。

练习册系列答案
相关题目

 时,求直线AN的解析式.
时,求直线AN的解析式.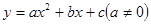 的图象如图所示, 其中对称轴为:x=1,则下列4个结论中正确的结论有( )个
的图象如图所示, 其中对称轴为:x=1,则下列4个结论中正确的结论有( )个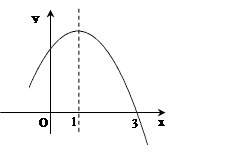
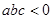 ; ②
; ② 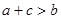 ;③
;③ 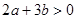 ; ④
; ④ 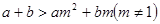 ;⑤
;⑤ 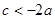 .
. 的图象如图所示,那么二次函数
的图象如图所示,那么二次函数 的图象大致为( )
的图象大致为( )

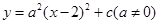 ,当自变量x分别取0,
,当自变量x分别取0,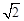 ,3时,对应的值分别为
,3时,对应的值分别为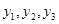 ,则
,则 的对称轴是直线
的对称轴是直线 ,且经过点
,且经过点 (3,0),则
(3,0),则 的值为( )
的值为( )

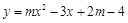 (m为常数)的图象经过原点,则m= .
(m为常数)的图象经过原点,则m= .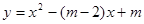 的图象过点(-1,15),
的图象过点(-1,15), =3,求点C的坐标。
=3,求点C的坐标。