题目内容
（1）如图1，在△ABC中，∠B、∠C均为锐角，其对边分别为b、c，求证：
=
；
（2）在△ABC中，AB=
，AC=
，∠B=45°，问满足这样的△ABC有几个在图2中作出来（不写作法，不述理由）并利用（1）的结论求出∠ACB的大小．
| b |
| sinB |
| c |
| sinC |
（2）在△ABC中，AB=
| 3 |
| 2 |
（1）证明：过A作AD⊥BC，垂足为D，
在Rt△ABD中，AD=csinB，
在Rt△ACD中，AD=bsinC，
csinB=bsinC，
故
=
．
（2）满足条件的△ABC有两个．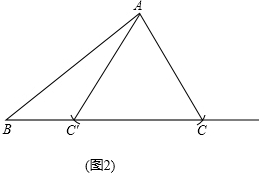
若∠ACB为锐角，由（1）的结论有
=
，
∴sinc=
，
∴∠ACB=60°；
若∠AC′C=∠ACC′=60°，
∴∠AC′B=120°．
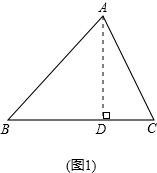
在Rt△ABD中，AD=csinB，
在Rt△ACD中，AD=bsinC，
csinB=bsinC，
故
| b |
| sinB |
| c |
| sinc |
（2）满足条件的△ABC有两个．
若∠ACB为锐角，由（1）的结论有
| ||
| sin45° |
| ||
| sinc |
∴sinc=
| ||
| 2 |
∴∠ACB=60°；
若∠AC′C=∠ACC′=60°，
∴∠AC′B=120°．
练习册系列答案
相关题目
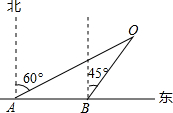计算说明．（供选用数据：
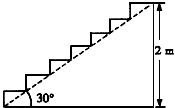
30°，已知原台阶坡面AB的长为5m（BC所在地面为水平面）．
