题目内容
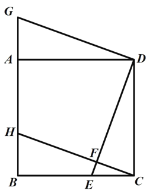
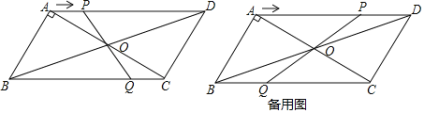
【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)当t=3时四边形OQCD的面积为多少?
【答案】(1)当t=2.5s时,四边形ABQP是平行四边形;(2)四边形OQCD面积=4.8cm2;
【解析】
(1)求出AP=BQ和AP∥BQ,根据平行四边形的判定得出即可;
(2)求出高AM和ON的长度,求出△DOC和△OQC的面积,再求出答案即可.
解:(1)当t=2.5s时,四边形ABQP是平行四边形
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC, AO=CO,
∴∠PAO=∠QCO,
∴△APO≌△CQO(ASA),
∴AP=CQ=t
∴BQ=5-t
若四边形ABQP是平行四边形,则AP=BQ
∴t=5-t
∴t=2.5即当t=2.5s时,四边形ABQP是平行四边形;
(2)过A作AM⊥BC于M,过O作ON⊥BC于N,
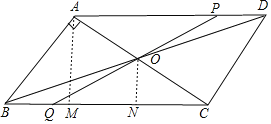
计算出AM=2.4(cm),ON=![]() =1.2cm,
=1.2cm,
△DOC的面积=![]()
当t=3s时,AP=CQ=3cm,
△OQC的面积为![]() cm2
cm2
∴四边形OQCD面积=3+1.8=4.8cm2.

练习册系列答案
相关题目