题目内容
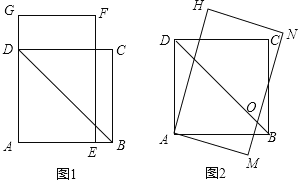
【题目】如图,在矩形纸片![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,把
上,把![]() 沿
沿![]() 翻折,
翻折,![]() 的落点是对角线
的落点是对角线![]() 上的点
上的点![]() 和
和![]() ,则四边形
,则四边形![]() 的面积是____________.
的面积是____________.
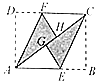
【答案】7.5
【解析】
直接根据矩形性质及平行四边形的判定证得四边形AECF是平行四边形,再根据勾股定理求出FC的长,最后利用平行四边形的面积公式计算即可得出结论.
解:∵翻折,
∴∠FAH=![]() ∠DAC,∠ECG=
∠DAC,∠ECG=![]() ∠BCA,
∠BCA,
∵四边形ABCD为矩形,
∴AD∥BC,AB∥CD,∠B=∠D=90°,
∴∠DAC=∠BCA,
∴∠FAH=∠ECG,
∴AF∥CE,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵在矩形纸片ABCD中,∠B=90°,AB=4,BC=3,
∴![]() ,
,
∵翻折,
∴∠FHA=∠D=90°,AH=AD=3,
同理可得,CG=3,
∴CH=AC-AH=5-3=2,
设DF=FH=x,则FC=4-x,
∵在Rt△FHC中,FC2=FH2+CH2,
∴(4-x)2=x2+22,
解得x=1.5,
∴FC=4-x=2.5,
∴四边形AECF的面积为FC·AD=2.5×3=7.5,
故答案为:7.5.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目