Question

【题目】如图，四边形 ABCD 是正方形，点 E，H 分别在 BC，AB 上，点 G 在 BA 的延长线上， 且 CE＝AG，DE⊥CH 于 F．

（1）求证：四边形 GHCD 为平行四边形．

（2）在不添加任何辅助线的情况下，请直接写出图中所有与∠ECF 互余的角．

Answer 1

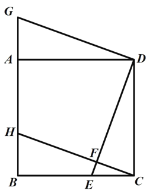
【答案】（1）见解析；（2）∠FEC，∠BHC，∠BGD，∠ADE，∠HCD

【解析】

（1）先证△ECD≌△GAD，得到∠EDC=∠ADG，再推到GD∥HC，从而证平行四边形；

（2）利用矩形顶角为90°，HC⊥ED，可推导∠BHC，∠HCD，∠FEC与∠ECF互余，再利用△ECD≌△GAD，可以推导得到∠BGD，∠ADE与∠ECF互余.

∵四边形ABCD是正方形，∴∠ECD=∠GAD=90°，CD=AD，HG∥CD

∵EC=AG

在△ECD和△GAD

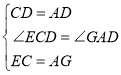
∴△ECD≌△GAD（SAS）

∴∠EDC=∠GDA

∵∠ADE+∠EDC=90°

∴∠GDA+∠ADE=90°

∵HC⊥ED，∴∠HFD=90°

∴GD∥HC

∴四边形GHCD是平行四边形

（2）∵∠BCD=90°，∴∠HCD与∠ECF互余

∵ED⊥HC，∴∠FEC与∠ECF互余

∵∠B=90°，∴∠BHC与∠ECF互余

∵△ECD≌△GAD，∴∠BGD=∠CED，∴∠BGD与∠ECF互余

∵已证∠GDF=90°，∴∠ADE与∠ECF互余