Question

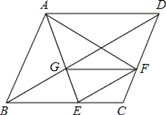
【题目】如图(1), 点为直线上一点，过点作射线, 将一直角的直角项点放在点处，即反向延长射线,得到射线.

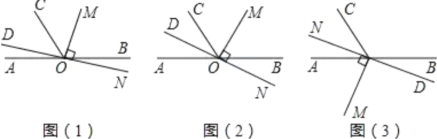
(1)当的位置如图(1)所示时，使，若，求的度数.

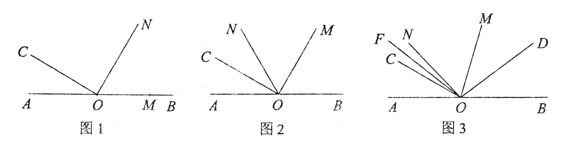
(2)当的位置如图(2)所示时，使一边在的内部，且恰好平分,

问:射线的反向延长线是否平分请说明理由：注意:不能用问题中的条件

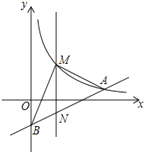
(3)当的位置如图所示时，射线在的内部，若.试探究与之间的数量关系，不需要证明，直接写出结论.

Answer 1

【答案】为；平分，理由见解析；

【解析】

(1)∠NOB+∠BOC+∠COD=180°，根据题目已知条件代入即可求解；

(2) ∠MON=∠MOD=90°，利用互余的性质可以得出∠DOC=∠BON，由对顶角的性质得出∠BON=∠AOD，即可得出结果；

(3)根据∠BOC=120°，得出∠AOC=60°，再利用∠MON-∠AOC=30°即可得出结论.

解：(1)∵∠NOB=20°，∠BOC=120°

∠NOB+∠BOC+∠COD=180°

∴∠COD=180°-20°-120°=40°

(2)OD平分∠AOC

∵∠MON=∠MOD=90°

∴∠DOC+COM=∠MOB+∠BON

∵OM平分∠BOC

∴∠COM=∠MOB

∴∠DOC=∠BON

∵∠BON=∠AOD（对顶角相等）

∴∠AOD=∠DOC

∴OD平分∠AOC

(3)∵∠BOC=120°

∴∠AOC=180°-120°=60°

∵∠MON=90°

∴∠MON-∠AOC=30°

∴∠AOM+∠AON-∠AON-∠NOC=30°

∴∠AOM-∠NOC=30°