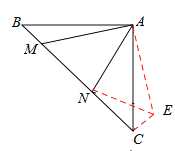
题目内容
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)证△ADG≌△ABE,△FAE≌△GAF,根据全等三角形的性质求出即可.
(2)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.通过证明△ABM≌△ACE(SAS)推知全等三角形的对应边AM=AE、对应角∠BAM=∠CAE;然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°,所以△MAN≌△EAN(SAS),故全等三角形的对应边MN=EN;最后由勾股定理得到EN2=EC2+NC2即MN2=BM2+NC2.
试题解析:解:(1)证明:∵四边形ABCD是正方形,∴∠ABE=∠ADG,AD=AB.
在△ABE和△ADG中,∵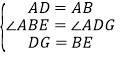 ,
,
∴△ABE≌△ADG(SAS).∴∠BAE=∠DAG,AE="AG." ∴∠EAG=90°.
在△FAE和△GAF中,∵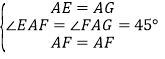 ,
,
∴△FAE≌△GAF(SAS),∴EF=FG.
(2)如答图,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM,连接AE、EN.
∵AB=AC,∠BAC=90°,∴∠B=∠C=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,∵ ,
,
∴△ABM≌△ACE(SAS).∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
∴由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,∵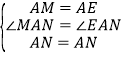 ,∴△MAN≌△EAN(SAS).∴MN=EN.
,∴△MAN≌△EAN(SAS).∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.∴MN2=BM2+NC2.
∵BM=1,CN=3,∴MN2=12+32. ∴MN=![]() .
.