Question

【题目】定义：直线y=ax+b与直线y=bx+a互为“友好直线”．如：直线y=2x+1与直线y=x+2互为“友好直线”.

（1）点M(m,2)在直线y=-x+4的“友好直线”上，则m=________；

（2）直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点，求点M的坐标；

（3）对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上，求直线y=ax+b的解析式．

Answer 1

【答案】

【解析】(1)、首先得出y=－x+4的“友好直线”，然后将点M代入得出答案；(2)、根据题意得出y=4x+3的“友好直线”，然后将点M代入列出方程组，从而得出答案；(3)、根据题意得出am+b=n和2bm+a=m-2n，然后化简得出（2b+2a-1）m=-a-2b，列成方程组，从而得出答案．

(1)、

(2)、由题意知，y=4x+3的“友好直线”是y=3x+4，

又∵点M(m,n)是直线y=4x+3上的点，又是它的“友好直线”上的点，∴

∴解得， ∴点M(1，7)；

(3)、∵点M(m,n)是直线y=ax+b上的任意一点， ∴am+b=n ①

∵点N(2m,m-2n)是直线y=ax+b的“友好直线”上的一点， ∴2bm+a=m-2n ②

将①代入②得：2bm+a=m-2(am+b)， 整理得：2bm+2am-m=-a-2b，

∴（2b+2a-1）m=-a-2b， ∵对于任意一点M(m,n)等式均成立， ∴，

解得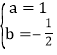， ∴y=x-．