题目内容
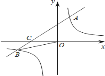
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .一次函数的图象分别交
.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
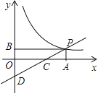
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式:
(3)根据图象写出当![]() 时,一次函数的值小于反比例函数的值的
时,一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3) ![]() .
.
【解析】
(1)由一次函数y=kx+b可知,D点坐标为(0,b),即OD=-b,结合tan∠ACP=![]() ,S△PAC=1,求出b的值,D点的坐标即可求出;
,S△PAC=1,求出b的值,D点的坐标即可求出;
(2)在Rt△ODC,tan∠OCD=tan∠ACP=![]() ,再求出P点坐标,于是可以求出一次函数与反比例函数的解析式;
,再求出P点坐标,于是可以求出一次函数与反比例函数的解析式;
(3)由两函数的图象直接写出x的取值范围即可。
解:(1)由一次函数![]() 可知,
可知,![]() 点坐标为
点坐标为![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() 点坐标为
点坐标为![]() ;
;
(2)在![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() ,
,
∴一次函数与反比例函数的解析式分别为![]() 、
、![]() ;
;
(3)由图象可知,一次函数与反比例函数图象的交点为![]() ,当
,当![]() 时一次函数的值小于反比例函数的值.
时一次函数的值小于反比例函数的值.
故答案为:(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3) ![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目