题目内容
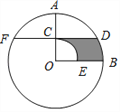
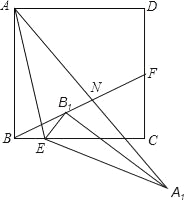
【题目】如图,正方形ABCD中,AB=4,点E是BC上一点,且tan∠BAE=![]() ,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
(1)求证:∠BFC=∠A1 B1F;
(2)说明点N是AA1的中点;
(3)求AN的长.
【答案】(1)详见解析; (2)详见解析;(3)![]() .
.
【解析】试题分析:(1)已知四边形ABCD是正方形,根据正方形的性质可得AB∥CD,即可得∠ABF=∠CFB,由旋转的性质可得EB=EB1,根据等腰三角形的性质可得∠EBB1=∠EB1B,再由∠ABC=∠EB1A1=90°,即可得∠ABF+∠EBB′=90°,∠BB1E+∠A1B1F=90°,所以∠A1B1F=∠ABF=∠BFC;(2)作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,可得点P是BB1的中点,根据三角形的中位线定理可得EP∥MB1,即可得MB1⊥BB1;易证△BPE∽△BCF,即可求得BP=![]() ,EP=
,EP=![]() ,从而求得BB1=
,从而求得BB1=![]() ,再证明A,B1,M三点共线,即可得AB1=
,再证明A,B1,M三点共线,即可得AB1=![]() ,再证明△AB1N≌△A1QN,即可得AN=A1N,从而证得N是AA1的中点;(3)由△AB1N≌△A1QN,可得B1N=
,再证明△AB1N≌△A1QN,即可得AN=A1N,从而证得N是AA1的中点;(3)由△AB1N≌△A1QN,可得B1N=![]() B1Q=
B1Q=![]() ,根据勾股定理即可求得AN=
,根据勾股定理即可求得AN=![]() .
.
试题解析:
(1)∵四边形ABCD是正方形,
∴AB∥CD,
∴∠ABF=∠CFB,
∵EB=EB1,
∴∠EBB1=∠EB1B,
∵∠ABC=∠EB1A1=90°,
∴∠ABF+∠EBB′=90°,∠BB1E+∠A1B1F=90°,
∴∠A1B1F=∠ABF=∠BFC.
(2)作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,
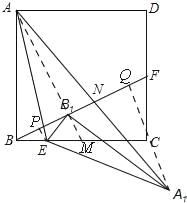
∴点P是BB1的中点,
∵E是BM中点,
∴EP∥MB1,
∴MB1⊥BB1,
由旋转得,△BPE∽△BCF,
∴BP=![]() ,EP=
,EP=![]() ,
,
∵PB1=PB=![]() ,
,
∴BB1=![]() ,
,
∵sin∠FBC=![]() =
=![]() =
=![]() ,
,
∴∠AB1B=90°,
∴A,B1,M三点共线,
∴AB1=![]() ,
,
∵∠B1A1Q=∠BB1E=∠FBC,
∴△B1QA1∽△FCB,
∴B1Q=![]() ,A1Q=
,A1Q=![]() =AB1,
=AB1,
∴△AB1N≌△A1QN,
∴AN=A1N,
∴N是AA1的中点.
(3)∵△AB1N≌△A1QN,
∴B1N=![]() B1Q=
B1Q=![]() ,
,
根据勾股定理得,AN=![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案