题目内容
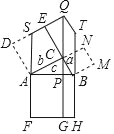
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
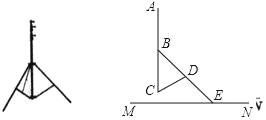
【答案】(40+30![]() )cm
)cm
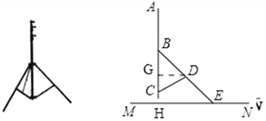
【解析】分析:过点D作DG⊥BC于点G,延长AC交MN于点H,则AH⊥MN,在Rt△DCG中,求出DG的值,在Rt△BDG中,求出BD的值,在Rt△BHE中,求出BH的值,从而结论可求.
详解:过点D作DG⊥BC于点G,延长AC交MN于点H,则AH⊥MN,
在Rt△DCG中,根据sin∠GCD=![]() ,得DG=CDsin∠GCD=
,得DG=CDsin∠GCD=![]() ,
,
在Rt△BDG中,根据sin∠GBD=![]() ,得
,得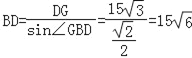 ,
,
∵D为BE的中点,
∴BE=2BD=30![]() ,
,
在Rt△BHE中,根据cos∠HBE=![]() ,
,
得BH=BE![]() ,
,
∴AH=AB+BH=40+30![]() ,
,
∴脚架BE的长度为30![]() cm,支架最高点A到地面
cm,支架最高点A到地面
的距离为(![]() )cm.
)cm.

练习册系列答案
相关题目