题目内容
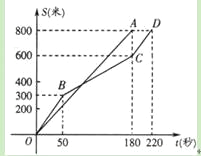
【题目】如图，直线y=k1x+b与双曲线y=
交于A、B两点，其横坐标分别为1和5，则不等式k1x＜+b的解集是_____．
【答案】﹣5＜x＜﹣1或x＞0
【解析】分析：根据不等式与直线和双曲线解析式的关系，相当于把直线向下平移2b个单位，然后根据函数的对称性可得交点坐标与原直线的交点坐标关于原点对称，再找出直线在双曲线下方的自变量x的取值范围即可．
详解：由k1x＜
+b，得，k1x-b＜，
所以，不等式的解集可由双曲线不动，直线向下平移2b个单位得到，
直线向下平移2b个单位的图象如图所示，交点A′的横坐标为-1，交点B′的横坐标为-5，
当-5＜x＜-1或x＞0时，双曲线图象在直线图象上方，
所以，不等式k1x＜+b的解集是-5＜x＜-1或x＞0．
故答案为：-5＜x＜-1或x＞0．
练习册系列答案
相关题目
【题目】有这样一个问题：探究函数
的图象与性质．
小华根据学习函数的经验，对函数
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数
的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | … |
y | … |
|
|
|
|
| 6 | 6 |
|
|
|
| m | … |
求m的值；
（3）如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；
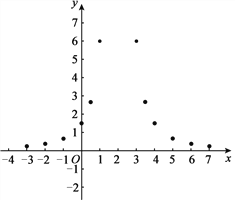
（4）结合函数的图象，写出该函数的一条性质： .
