题目内容
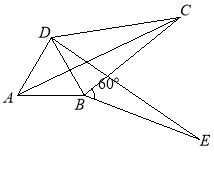
【题目】如图,在平面直角坐标系中,已知A(﹣2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
(1)求点O′的坐标;
(2)已知抛物线y=ax2+bx+c过A,B,C三点,且与⊙O′交于另一点E,求抛物线的解析式,并直接写出点E 坐标;
(3)设点P(t,0)是线段OB上一个动点,过点P作直线l⊥x轴,交线段BC于F,交抛物线y=ax2+bx+c于点G,请用t表示四边形BPCG的面积S;
(4)在(3)的条件下,四边形BPCG能否为平行四边形?若能,请求出t的值;若不能,请说明理由.
【答案】
(1)解:如图1中,连接CO′,设⊙O′的半径为R.

在Rt△OCO′中,∵OC2+OO2=CO′2,
∴42+(R﹣2)2=R2,
∴R=5,
∴OO′=5﹣2=3,
∴O′(3,0).
(2)解:∵A(﹣2,0),C(0,4),B(8,0),
∴  ,解得
,解得 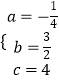 ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4.
x+4.
易知E、C关于对称轴对称,
∴点E的纵坐标为4,
∴E(6,4)
(3)解:由题意G(t,﹣ ![]() t2+
t2+ ![]() t+4),
t+4),
∴S四边形BPCG= ![]() PG(Bx﹣Cx)=
PG(Bx﹣Cx)= ![]() (﹣
(﹣ ![]() t2+
t2+ ![]() t+4)8=﹣t2+6t+16(0<t<8)
t+4)8=﹣t2+6t+16(0<t<8)
(4)解:不可能是平行四边形.
理由:假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB﹣OP=2,
∴CE≠BP,
∴四边形BPCG不可能是平行四边形.
【解析】(1)如图1中,连接CO′,设⊙O′的半径为R.在Rt△OCO′中,根据OC2+OO2=CO′2,可得42+(R-2)2=R2,解方程求出求点O′的坐标;
(2)把A(-2,0),C(0,4),B(8,0)代入抛物线抛物线y=ax2+bx+c,求抛物线的解析式即点E 坐标;
(3)根据S四边形BPCG=![]() PG(Bx-Cx),即可用t表示四边形BPCG的面积S
PG(Bx-Cx),即可用t表示四边形BPCG的面积S
(4)不可能是平行四边形.假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,推出CE≠BP,即可得到所求结论..
【考点精析】本题主要考查了勾股定理的概念和平行四边形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

【题目】为积极支持鄂州市创建国家卫生城市工作,某商家计划从厂家采购A,B两种清洁产品共20件,产品的采购单价(元/件)是采购数量(件)的相关信息如下表所示.
采购数量(件) | 2 | 4 | 6 | … |
A产品单价(元) | 1460 | 1420 | 1380 | … |
B产品单价(元) | 1280 | 1260 | 1240 | … |
(1)设B产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大?并求最大利润.