题目内容
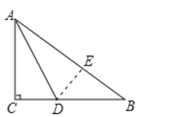
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,BD=4cm,CD=2cm,
(1)求D点到直线AB的距离.
(2)求AC.

【答案】(1)2cm;(2)2![]() .
.
【解析】
(1)作DE⊥AB,由角平分线的性质知CD=DE=2,故为D点到直线AB的距离;
(2)∵BD=4,DE=2,∠BED=90°,故∠B=30°,
再根据BC=6,AB=2AC与勾股定理即可求出AC的长.
(1)作DE⊥AB,
∵AD平分∠CAB,DE⊥AB,CD⊥AC
∴CD=DE=2,故为D点到直线AB的距离;
(2)∵BD=4,DE=2,∠BED=90°,
∴∠B=30°,
∴AB=2AC
设AC=x,则AB=2x,
由AB2=AC2+BC2,
(2x)2=x2+62,
解得x=2![]() .
.

【题目】根据《中华人民共和国个人所得税法》,新个税标准将于2019年1月1日起施行.其中每月纳税的起征点增加到5000元,即2019年1月以后每月工资中的5000元将不必缴纳税款.根据相关政策,纳税部门给大家制作了如下纳税表格(未完整):
级数 | 全月应纳税所得额(含税级距) | 税率( | 速算扣除数 |
1 | 不超过3000元的部分 |
| 0 |
2 | 超过3000元至12000元的部分 |
| 210 |
3 | 超过12000元至25000元的部分 |
| 1410 |
4 | 超过25000元至35000元的部分 |
|
|
5 | 超过35000元至55000元的部分 |
| 4410 |
6 | 超过55000元至80000元的部分 |
| 7160 |
7 | 超过80000元的部分 |
| 15160 |
例如:张三2019年1月如果月收入为21000元,则他1月中的![]() 元应该纳税,纳税数额为:
元应该纳税,纳税数额为:![]() (元).
(元).
(1)如果李士业2019年1月份收入为7000元,则他1月份应纳税多少元?
(2)如果王努利2019年1月份收入为10000元,则他月份应纳税多少元?
(3)钱勒凤跟朋友说,估计自己1月份应纳税3400元,则钱勤奋1月份收入约有多少元?
(4)根据表中各数据关系,求表格中的![]() ,
,![]() 的值.
的值.