Question

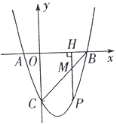
【题目】如图，抛物线y＝ax2﹣11ax+24a交x轴于C，D两点，交y轴于点B（0，），过抛物线的顶点A作x轴的垂线AE，垂足为点E，作直线BE．

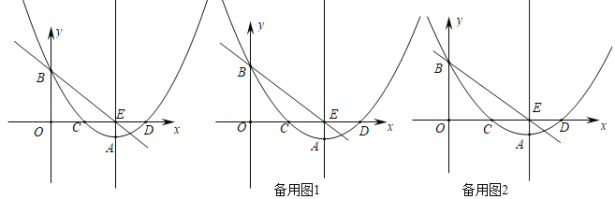
（1）求直线BE的解析式；

（2）点H为第一象限内直线AE上的一点，连接CH，取CH的中点K，作射线DK交抛物线于点P，设线段EH的长为m，点P的横坐标为n，求n与m之间的函数关系式．（不要求写出自变量m的取值范围）；

（3）在（2）的条件下，在线段BE上有一点Q，连接QH，QC，线段QH交线段PD于点F，若∠HFD＝2∠FDO，∠HQC＝90°∠FDO，求n的值．

Answer 1

【答案】（1）yx；（2）nm+3；（3）或

【解析】

（1）根据抛物线可得对称轴，可知点E的坐标，利用待定系数法可得一次函数BE的解析式；

（2）如图1，作辅助线，构建直角三角形，根据抛物线过点B（0，），可得a的值，计算y＝0时，x的值可得C和D两点的坐标，从而知CD的值，根据P的横坐标可表示其纵坐标，根据tan∠PDM，

tan∠KDN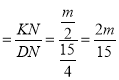，相等列方程为，可得结论；

（3）如图2，延长HF交x轴于T，先根据已知得∠FDO＝∠FTO，由等角的三角函数相等和（2）中的结论得：tan∠FDO＝tan∠FTO，则，可得ET和CT的长，令∠FDO＝∠FTO＝2α，表示角可得∠TCQ＝∠TQC，则TQ＝CT＝5，

设Q的坐标为（t，t），根据定理列方程可得：TS2+QS2＝TQ2，（2+t）2+（）2＝52，解得t1，t2＝1；根据两个t的值分别求n的值即可．

解：（1）∵抛物线y＝ax2﹣11ax+24a，

∴对称轴是：x，

∴E（，0），

∵B（0，），

设直线BE的解析式为：y＝kx+b，

则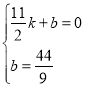，解得：，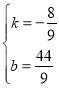

∴直线BE的解析式为：yx；

（2）如图1，过K作KN⊥x轴于N，过P作PM⊥x轴于M，

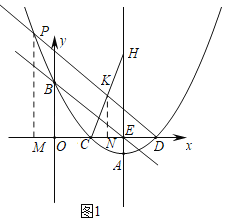
∵抛物线y＝ax2﹣11ax+24a交y轴于点B（0，），

∴24a，

∴a，

∴yx2x（x﹣3）（x﹣8），

∴当y＝0时，（x﹣3）（x﹣8）＝0，

解得：x＝3或8，

∴C（3，0），D（8，0），

∴OC＝3，OD＝8，

∴CD＝5，CE＝DE，

∴P点在抛物线上，

∴P[n，（n﹣3）（n﹣8）]，

∴PM（n﹣3）（n﹣8），DM＝8﹣n，

∴tan∠PDM，

∵AE⊥x轴，

∴∠KNC＝∠HEC＝90°，

∴KN∥EH，

∴1，

∴CN＝ENCE，

∴KNm，ND，

在△KDN中，tan∠KDN中，tan∠KDN，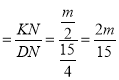

∴，

nm+3；

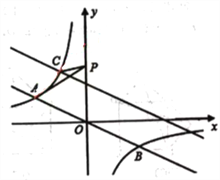
（3）如图2，延长HF交x轴于T，

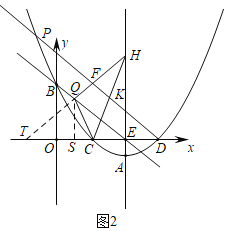
∵∠HFD＝2∠FDO，∠HFD＝∠FDO+∠FTO，

∴∠FDO＝∠FTO，

∴tan∠FDO＝tan∠FTO，

在Rt△HTE中，tan∠FTO，

∴，

∴ET，

∴CT＝5，

令∠FDO＝∠FTO＝2α，

∴∠HQC＝90°，

∴∠TQC＝180°﹣∠HQC＝90°﹣α，∠TCQ＝180°﹣∠HTC﹣∠TQC＝90°﹣α，

∴∠TCQ＝∠TQC，

∴TQ＝CT＝5，

∵点Q在直线yx上，

∴可设Q的坐标为（t，t），

过Q作QS⊥x轴于S，则QSt，TS＝2+t，

在Rt△TQS中，TS2+QS2＝TQ2，

∴（2+t）2+（）2＝52，

解得t1，t2＝1；

①当t时，QS，TS，

在Rt△QTH中，tan∠QTS，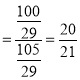

∴，m，

∴n3，

②当t＝1时，QS＝4，TS＝3，

在Rt△QTH中，tan∠QTS，

∴，

m＝10，

∴n3．