题目内容
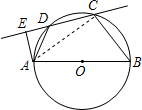
如图，四边形ABCD为⊙O内接四边形，AB为直径，过点A作直线CD的垂线，垂足为E．若AB=5，BC=3，则tan∠DAE的值是______．
连接AC，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CAB+∠ABC=90°，
∵AB=5，BC=3，
∴AC=
=
=4，
∵四边形ABCD为⊙O内接四边形，
∴∠ADE=∠ABC，
∵AE⊥CD，
∴∠AED=90°，
∴∠DAE+∠ADE=90°，
∴∠DAE=∠CAB，即tan∠DAE=tan∠CAB=
=
．
故答案为：
．
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CAB+∠ABC=90°，
∵AB=5，BC=3，
∴AC=
| AB2-BC2 |
| 52-32 |
∵四边形ABCD为⊙O内接四边形，
∴∠ADE=∠ABC，
∵AE⊥CD，
∴∠AED=90°，
∴∠DAE+∠ADE=90°，
∴∠DAE=∠CAB，即tan∠DAE=tan∠CAB=
| BC |
| AC |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
练习册系列答案
口算能手系列答案
相关题目
