Question

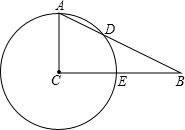
如图，AB是⊙O的直径，C、D是⊙O上的两点，且AC=CD．
（1）求证：OC∥BD；
（2）若BC将四边形OBDC分成面积相等的两个三角形，试确定四边形OBDC的形状．

Answer 1

（1）证明：∵AC=CD，
∴弧AC与弧CD相等，
∴∠ABC=∠CBD，
又∵OC=OB（⊙O的半径），
∴∠OCB=∠OBC，
∴∠OCB=∠CBD，
∴OC∥BD；

（2）∵OC∥BD，
不妨设平行线OC与BD间的距离为h，
又S_△OBC=

1

2

OC×h，S_△DBC=

1

2

BD×h，
因为BC将四边形OBDC分成面积相等的两个三角形，
即S_△OBC=S_△DBC，
∴OC=BD，
∴四边形OBDC为平行四边形，
又∵OC=OB，
∴四边形OBDC为菱形．