题目内容
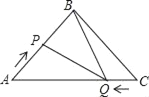
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)是否存在某一时刻,使![]() ?若存在,求出此时
?若存在,求出此时![]() 的长;若不存在,请说理由;
的长;若不存在,请说理由;
(3)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)当x=![]() 时,PQ∥BC;(2)存在,AP=
时,PQ∥BC;(2)存在,AP=![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
(1)由PQ∥BC,得出比例式![]() ,即可求出x的值;
,即可求出x的值;
(2)由BA=BC得∠A=∠C.要使△APQ∽△CQB,只需![]() ,此时
,此时![]() 解这个方程就可解决问题.
解这个方程就可解决问题.
(3)当CQ=10时,可求出x,从而求出AP,即可求出BP,然后根据两个三角形两底上的高相等时,这两个三角形的面积比等于这两个底的比,就可解决问题;
解:(1)由题可得AP=4x,CQ=3x.
∵BA=BC=20,AC=30,
∴BP=20﹣4x,AQ=30﹣3x.
若PQ∥BC,
则有△APQ∽△ABC,
∴![]()
∴![]()
解得:x=![]() .
.
∴当x=![]() 时,PQ∥BC;
时,PQ∥BC;
(2)存在.
∵BA=BC,∴∠A=∠C.
要使△APQ∽△CQB,
只需![]()
此时![]()
解得:x=![]() ,
,
∴AP=4x=![]() ;
;
(3)当CQ=10时,3x=10,
∴x=![]() ,
,
∴AP=4x=![]() ,
,
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目