Question

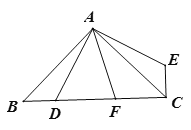
【题目】如图，海中有一小岛A，它周围8海里内有暗礁，渔船由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测得小岛A在北偏东30°方向上．

(1)求∠BAD的度数；

(2)如果渔船不改变航线继续向东航行，有没有触礁的危险？

Answer 1

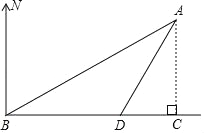
【答案】(1)30°；(2)没有触礁的危险．

【解析】

(1)过A作AC⊥BD于点C，求出∠CAD、∠CAB的度数，求出∠BAD和∠ABD

(2)根据等边对等角得出AD=BD=12，根据含30度角的直角三角形性质求出AC即可．

解：(1)∵∠CAD＝30°，∠CAB＝60°，

∴∠BAD＝60°﹣30°＝30°．

(2)过A作AC⊥BD于点C，则AC的长是A到BD的最短距离．

∵∠ABD＝90°﹣60°＝30°．

∴∠ABD＝∠BAD．

∴BD＝AD＝12海里．

∵Rt△ACD中，∠CAD＝30°，

∴AC＝ADcos∠CAD＝≈10.392＞8，

即渔船继续向正东方向行驶，没有触礁的危险．