题目内容
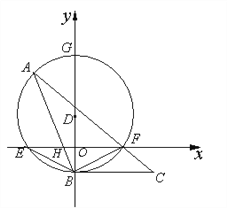
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
【答案】(1)直线BC与⊙D相切,理由见解析;
(2)证明见解析;
(3)F(4,0),A(-4.8,4.4)
【解析】试题分析:(1)连FG,要证BC是切线,只需证∠DBC=90°,即证∠DBF+∠CBF=90°,而∠CBF=∠A,∠A=∠BGF,又∠BGF+∠DBF=90°,则可证明.
(2)连AE,则得到母子三角形的基本图形,结合垂径定理和圆周角定理证明△BEH∽△BAE即可.
(3)求坐标,作垂线,所以过点A分别向坐标轴作垂线,结合相似三角形的性质求出AQ,OQ的长即可.
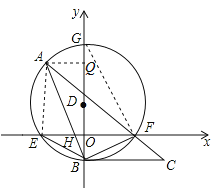
试题解析(1)直线BC与⊙D相切.
证明:如图,连接GF,∵BG是⊙D直径,∴∠GFB=90°.
∴∠G+∠GBF=90°,
∵∠A=∠G ,∠FBC=∠A,∴∠G=∠FBC,
∴∠FBC+∠GBF=90°,即∠GBC=90°,
∴直线BC与⊙D相切.
(2) 如图,连接AE.
∵BG⊥EF, BG是⊙D直径.
∴![]() ,∴∠BEH=∠BAE ,∵∠BAE=∠EAH , ∴△BEH∽△BAE.
,∴∠BEH=∠BAE ,∵∠BAE=∠EAH , ∴△BEH∽△BAE.
∴![]() ∴BE2=BH·AB.
∴BE2=BH·AB.
(3) 作AQ⊥GB,∵E(-4,0),根据垂径定理得,OE=OF=4,∴F(4,0) .
∵BE2=BH·AB, BE2=OE2 +OB2=16+4=20, AB=8,∴BH=2.5,得OH=1.5 .
由△BOH∽△BQA,得![]() AQ=4.8,BQ=6.4.
AQ=4.8,BQ=6.4.
∴OQ=4.4 ,∴A(-4.8,4.4).

 阅读快车系列答案
阅读快车系列答案