题目内容
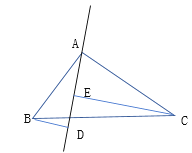
【题目】如图1，在平面直角坐标系中，等腰
的斜边OB在x轴上，直线
经过等腰的直角顶点A，交y轴于C点，双曲线
也经过A点
连接BC．
求k的值；
判断
的形状，并求出它的面积．
若点P为x正半轴上一动点，在点A的右侧的双曲线上是否存在一点M，使得
是以点A为直角顶点的等腰直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．
【答案】（1）
；（2）
是直角三角形，S△ABC=8；
（3）在双曲线上存在一点
，使得
是以点A为直角顶点的等腰三角形.
【解析】
（1）过点A分别作
轴于M点，
轴于N点，根据直角三角形的性质可设点A的坐标为
，因为点A在直线
上，即把A点坐标代入解析式即可算出a的值，进而得到A点坐标，然后再利用待定系数法求出反比例函数解析式；
（2）利用勾股定理逆定理即可判断出三角形ABC是直角三角形，再利用三角形面积公式求解即可；
（3）由“边角边”易证
≌
，得出
，那么
是所求的等腰直角三角形，再根据全等三角形的性质及函数图象与点的坐标的关系得出结果．
解：
如图1，
过点A分别作
轴于Q点，轴于N点，
是等腰直角三角形，
，
设点A的坐标为
，
点A在直线
上，
，
解得
，
则点A的坐标为
，
双曲线
也经过A点，
；
由知，
，
，
直线与y轴的交点为C，
，
，
，
，
是直角三角形；
则S△ABC=
AB·BC=
；
如图2，
假设双曲线上存在一点M，使得是等腰直角三角形；
，
，
连接AM，BM，
由知，，
反比例函数解析式为
，
，
在
和
中，
，
≌
，
，
，
点M的横坐标为4，
；
即：在双曲线上存在一点，使得是以点A为直角顶点的等腰三角形.
练习册系列答案
相关题目
