��Ŀ����
����Ŀ��ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ����ѧ���������Ȥ�����������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��

��1������ε����У�ϲ��������Ŀ��ͬѧ���� ���ˣ�������ͳ��ͼ�У���ƹ�������İٷֱ�Ϊ�� ��%�����ѧУ��800��ѧ��������ȫУѧ�������� ����ϲ��������Ŀ��
��2���뽫����ͳ��ͼ����������
��3���ڱ������ѧ���У�ϲ���������2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ�����༶�μ�У����ӣ���ֱ��д������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
���𰸡���1��5��20��80����2��ͼ����������3��![]() .
.
�������������������1������������������������ռ�İٷֱȼ����������������������������ֱ��ȥϲ��������Ŀ�������ɵõ�ϲ��������Ŀ���������ټ����ϲ��ƹ������Ŀ�İٷֱȣ�Ȼ����800����������ϲ��������Ŀ�İٷֱȿɹ���ȫУѧ����ϲ��������Ŀ��������
��2�����ݣ�1������õ����ݿɲ�������ͳ��ͼ��
��3������״ͼչʾ����20�ֵȿ��ܵĽ���������ҳ�����ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�Ľ������Ȼ����ݸ��ʹ�ʽ���.
�����������1�������������Ϊ20��40%=50���ˣ���
����ϲ��������Ŀ��ͬѧ������=50��20��10��15=5���ˣ���
��ƹ�������İٷֱ�=![]() =20%��
=20%��
��Ϊ800��![]() =80��
=80��
���Թ���ȫУѧ������80��ϲ��������Ŀ��
�ʴ�Ϊ5��20��80��
��2����ͼ��
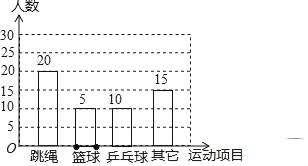
��3������״ͼΪ��

����20�ֵȿ��ܵĽ��������������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�Ľ����Ϊ12��
��������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ���=![]() =
=![]() ��
��