Question

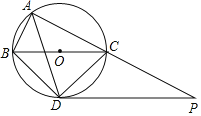
【题目】如图，在Rt△ABC中，∠C＝90°，AB＝8．

（1）作△ABC的内角∠CAB的平分线，与边BC交于点D（用尺规作图，保留作图痕迹，不要求写作法）；

（2）若AD＝BD，求CD的长度．

Answer 1

【答案】（1）见解析；（2）CD＝.

【解析】

（1）利用基本作图作∠BAC的平分线；

（2）利用等腰三角形的性质和三角形内角和计算出∠CAD＝∠B＝30°，在Rt△ACB中利用含30度的直角三角形三边的关系得到AC＝4，然后在Rt△ACD中求CD．

解：（1）如图，AD为所作；

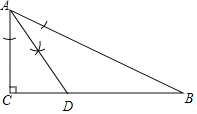
（2）∵AD＝BD，

∴∠DAB＝∠B，

∵AD平分∠BAC，

∴∠DAB＝∠CAD，

∴∠DAB＝∠CAD＝∠B，

而∠DAB+∠CAD+∠B＝90°，

∴∠CAD＝∠B＝30°，

在Rt△ACB中，AC＝AB＝4，

在Rt△ACD中，tan∠CAD＝，

∴CD＝4tan30°＝4×＝．