题目内容
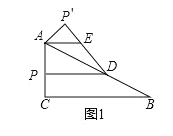
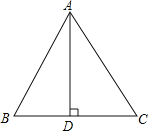
【题目】如图，在等边△ABC中，AB＝6，AD是高．
（1）尺规作图：作△ABC的外接圆⊙O（保留作图痕迹，不写作法）
（2）在（1）所作的图中，求线段AD，BD与弧
所围成的封闭图形的面积．
【答案】（1）见解析；（2）
【解析】
（1）作BH⊥AC交AD于O，以O为圆心，OB为半径作⊙O即可．
（1）线段AD，BD与
所围成的封闭图形的面积＝S扇形OAB+S△BOD．
解：（1）如图，⊙O即为所求．
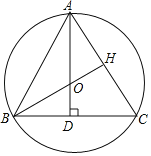
（2）∵△ABC是等边三角形，AD⊥BC，BH⊥AC，
∴BD＝CD＝3，∠OBD＝
∠ABC＝30°，∠AOB＝2∠C＝120°，
∴OD＝BDtan30°＝
，OB＝2OD＝2，
∴线段AD，BD与所围成的封闭图形的面积＝S扇形OAB+S△BOD＝
×3×＝2π+．
练习册系列答案
高中必刷题系列答案
相关题目
【题目】为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
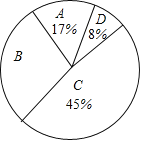
请根据所给信息，解答以下问题：
(1)表中a=___，b=___；
(2)请计算扇形统计图中B组对应扇形的圆心角的度数；
(3)已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
