题目内容
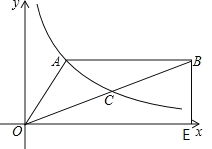
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(1)确定k的值;
(2)若点D(3,m)在双曲线上,求直线AD的解析式;
(3)计算△OAB的面积.
【答案】(1)k=6 (2) y=﹣x+5 (3) 9
【解析】试题分析:(1)将A坐标代入反比例解析式求出k的值即可;
(2)将D坐标代入反比例解析式求出m的值,确定出D坐标,设直线AD解析式为y=kx+b,将A与D坐标代入求出k与b的值,即可确定出直线AD解析式;
(3)过点C作CN⊥y轴,垂足为N,延长BA,交y轴于点M,得到CN与BM平行,进而确定出三角形OCN与三角形OBM相似,根据C为OB的中点,得到相似比为1:2,确定出三角形OCN与三角形OBM面积比为1:4,利用反比例函数k的意义确定出三角形OCN与三角形AOM面积,根据相似三角形面积之比为1:4,求出三角形AOB面积即可.
试题解析:(1)将点A(2,3)代入解析式y=![]() ,
,
得:k=6;
(2)将D(3,m)代入反比例解析式y=![]() ,
,
得:m=![]() =2,
=2,
∴点D坐标为(3,2),
设直线AD解析式为y=kx+b,
将A(2,3)与D(3,2)代入
得: ![]() ,
,
解得: ![]()
则直线AD解析式为y=-x+5;
(3)过点C作CN⊥y轴,垂足为N,延长BA,交y轴于点M,
∵AB∥x轴,
∴BM⊥y轴,
∴MB∥CN,
∴△OCN∽△OBM,
∵C为OB的中点,即![]() ,
,
∴![]() ,
,
∵A,C都在双曲线y=![]() 上,
上,
∴S△OCN=S△AOM=3,
由![]() ,
,
得:S△AOB=9,
则△AOB面积为9.

【题目】我市晶泰星公司安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品.根据市场行情测得,甲产品每件可获利
件乙产品.根据市场行情测得,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产
元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产![]() 件乙产品,当天每件乙产品平均荻利减少
件乙产品,当天每件乙产品平均荻利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?