题目内容
【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F,

(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG;
【答案】(1) ![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)易得:![]() ≌
≌ ![]()
![]() 即可求出
即可求出![]() 的度数.
的度数.
(2))在BF上取M使AF=FM,连MC延长FG交MC于N,可得△AFM是等边三角形,可证△AFB≌△AMC,再证△AGF≌△CGN,可得![]() 是
是![]() 的中点,可以根据等腰三角形三线合一的性质解答即可.
的中点,可以根据等腰三角形三线合一的性质解答即可.
解:(1)在等边△ABC中:AB=AC,∠BAK=∠C=60°
在△ABK和△CAH中,
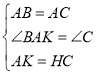
∴![]() ≌
≌ ![]()
![]()
![]()
(2)在BF上取M使AF=FM,连MC延长FG交MC于N,
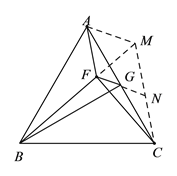
∵![]()
∴![]()
∴△AFM是等边三角形
∴AF=AM, ∠FAM=60°
又∵∠BAC=60°
∴∠BAF=∠CAM
又∵AB=AC
∴△AFB≌△AMC,
∴∠AMC=∠AFC= 120°,
又△AFM为等边三角形,
∴∠AMB=∠BMC=60°,
∵∠BFC=90°,
∴∠MFC=90°,∠NFC=30°,
∴△FMN为等边三角形,且FN=NC,
∴NC=FN=FM=AF,
∴△AGF≌△CGN,
∴AG=GC,
又∵AB=BC
∴BG⊥AC,

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目






