题目内容
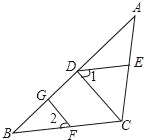
【题目】已知:在△ABC中,∠ABC=60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C. D重合),且∠EAC=2∠EBC.

(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB=___°,∠AEC=___°.
(2)如图2,①求证:AE+AC=BC;
②若∠ECB=30°,且AC=BE,求∠EBC的度数。
【答案】(1)27°,99°;(2)①见解析;②20°;
【解析】
(1)由等腰三角形的性质得到∠EBC=∠ECB=27°,根据角平分线的性质得到∠DEB=∠EBC+∠ECB=54°,再由角平分线的性质得到∠ACD=∠ECB=27°,因为∠EAC=2∠EBC=54°,求得∠AEC=180°-27°-54°=99°;
(2)①在BC上取一点M,使BM=ME,根据等腰三角形的性质得到∠MBE=∠MEB,由∠EAB=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,得到∠EAC=∠EMC,由全等三角形的性质推出AE=ME,CM=AC,于是得到结论;
②如图2,在BC上取一点M,使BM=ME,连接AM,由∠ECB=30°,得到∠ACB=60°,于是推出△AMC是等边三角形,通过三角形全等得到∠EBC=∠MAE,由∠MAC=60°,得到∠EAC=2∠EBC=2∠MAE,于是得出结果.
(1)∵EB=EC,
∴∠EBC=∠ECB=27°,
∵CD平分∠ACB,
∴∠ACD=∠ECB=27°,
∵∠EAC=2∠EBC=54°,
∴∠AEC=180°27°54°=99°,
故答案为:27°,99°;
(2)①证明:如图1,在BC上取一点M,使BM=ME,
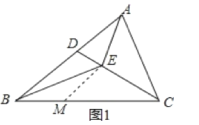
∴∠MBE=∠MEB,
∵∠EAC=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,
∴∠EAC=∠EMC,
在△ACE与△MCE中,
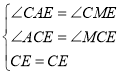 ,
,
∴△ACE≌△MCE,
∴AE=ME,CM=AC,
∴AE=BM,
∴BC=BM+CM=AE+AC;
②如图2在BC上取一点M,使BM=ME,连接AM,
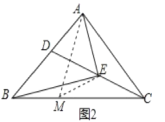
∵∠ECB=30°,
∴∠ACB=60°,由①可知;△AMC是等边三角形(M点与B点重合),
∴AM=AC=BE,
在△EMB与△MEA中,
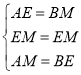 ,
,
∴∠EBC=∠MAE,
∵∠MAC=60°,
∵∠EAC=2∠EBC=2∠MAE,
∴∠MAE=20°,∠EAC=40°,
∴∠EBC=20°.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案