Question

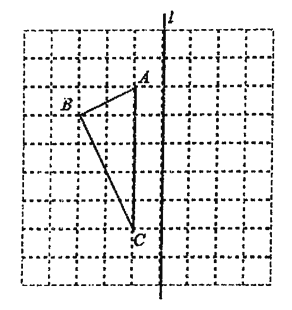
【题目】如图，抛物线 经过点 ，交y 轴于点C：

（1）求抛物线的解析式（用一般式表示）．
（2）点 为 轴右侧抛物线上一点，是否存在点 使 ，若存在请直接给出点 坐标；若不存在请说明理由．
（3）将直线 绕点 顺时针旋转 ，与抛物线交于另一点 ，求 的长．

Answer 1

【答案】
（1）

解：依题可得：

解得：

∴y=-x2+x+2.

（2）

解：依题可得：AB=5,OC=2,

∴S△ABC=AB×OC=×2×5=5.

∵S△ABC=S△ABD.

∴S△ABD=×5=.

设D（m,-m2+m+2）（m＞0）.

∵S△ABD=AB|yD|=.|

×5×|-m2+m+2|=.

∴m=1或m=2或m=-2（舍去）或m=5

∴D1（1，3），D2（2，3）,D3（5，-3）.

（3）

解：过C作CF⊥BC交BE于点F；过点F作FH⊥y轴于点H.

∵∠CBF=45°,∠BCF=90°.

∴CF=CB.

∵∠BCF=90°,∠FHC=90°.

∴∠HCF+∠BCO=90°,∠HCF+∠HFC=90°

∴∠HFC=∠OCB.
∵
∴△CHF≌△BOC（AAS）.

∴HF=OC=2,HC=BO=4,

∴F（2，6）.

设直线BE解析式为y=kx+b.

∴

解得

∴直线BE解析式为:y=-3x+12.

∴

解得：x1=5,x2=4（舍去）

∴E（5，-3）.

BE==.

【解析】（1）用待定系数法求二次函数解析式.
（2）依题可得：AB=5,OC=2,求出S△ABC=AB×OC=×2×5=5；根据S△ABC=S△ABD；求出S△ABD=×5=.
设D（m,-m2+m+2）（m＞0）.根据三角形的面积公式得到一个关于m的方程，求解即可.
（3）过C作CF⊥BC交BE于点F；过点F作FH⊥y轴于点H;根据同角的余角相等得到∠HFC=∠OCB；再根据条件得到△CHF≌△BOC（AAS）；利用其性质可求出HF=OC=2,HC=BO=4,从而得到F（2，6）；用待定系数法求直线BE解析式；再把抛物线解析式和直线BE解析式联立得到方程组求E点坐标，再根据勾股定理求出BE长.
【考点精析】本题主要考查了因式分解法和确定一次函数的表达式的相关知识点，需要掌握已知未知先分离，因式分解是其次．调整系数等互反，和差积套恒等式．完全平方等常数，间接配方显优势；确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能正确解答此题．