Question

【题目】如图一次函数 与反比例函数 交于 、 ，与 轴， 轴分别交于点 ．

（1）直接写出一次函数 的表达式和反比例函数 的表达式；
（2）求证： ．

Answer 1

【答案】
（1）

解：将A（2，4）代入y=.

∴ m=2×4=8.

∴ 反比例函数解析式为y=.

∴将B（a,1）代入上式得a=8.

∴B（8，1）.

将A（2，4）,B（8，1）代入y=kx+b得：

.

∴
∴一次函数解析式为：y=-x+5.

（2）

证明：由（1）知一次函数解析式为y=-x+5.

∴C（10，0），D（0，5）.

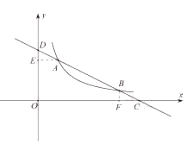
如图，过点A作AE⊥y轴于点E，过B作BF⊥x轴于点F.
∴E（0，4），F（8，0）.

∴AE=2,DE=1,BF=1,CF=2

∴在Rt△ADE和Rt△BCF中，根据勾股定理得：

AD==,BC==.

∴AD=BC.

【解析】（1）将A（2，4）代入y=求出m得到反比例函数解析式；再将B（a,1）代入得a，将A（2，4）,B（8，1）代入y=kx+b得一个二元一次方程组求解即可得一次函数解析式.
（2）由（1）可得C（10，0），D（0，5）；如图，过点A作AE⊥y轴于点E，过B作BF⊥x轴于点F；从而得到E（0，4），F（8，0）；
AE=2,DE=1,BF=1,CF=2在Rt△ADE和Rt△BCF中，根据勾股定理得AD=BC.
【考点精析】通过灵活运用确定一次函数的表达式和勾股定理的概念，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．