题目内容
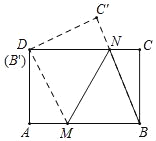
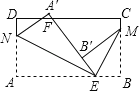
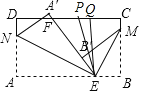
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)判断直线EN,ME的位置关系,并说明理由;
(2)设∠MEN的平分线EP交边CD于点P,∠MEN的一条三等分线EQ交边CD于点Q.求∠PEQ的度数.
【答案】(1)EN⊥ME,理由见解析;(2)15°.
【解析】
(1)首先由折叠的性质,得出∠AEN=∠A′EN,∠BEM=∠B′EM,再由∠AEN+∠A′EN+∠BEM+∠B′EM=180°,得出∠A′EN+∠B′EM=90°,进而即可得出EN⊥ME;
(2)首先根据EP平分∠MEN,∠MEN=90°,得出∠MEP=45°,然后再由三等分的性质得出∠MEQ=30°,进而得出∠PEQ.
(1)EN⊥ME,
理由:由折叠的性质得,∠AEN=∠A′EN,∠BEM=∠B′EM,
∵∠AEN+∠A′EN+∠BEM+∠B′EM=180°,
∴∠A′EN+∠B′EM=90°,
∴EN⊥ME;
(2)∵EP平分∠MEN,∠MEN=90°,
∴∠MEP=45°,
∵EQ三等分∠MEN,
∴∠MEQ=30°,
∴∠PEQ=∠MEP﹣∠MEQ=15°.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目