题目内容
【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点B(6,8),动点M,N同时从O点出发,点M沿射线OA方向以每秒1个单位的速度运动,点N沿线段OB方向以每秒0.6个单位的速度运动,当点N到达点B时,点M,N同时停止运动,连接MN,设运动时间为t(秒).
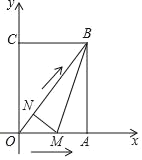
(1)求证△ONM~△OAB;
(2)当点M是运动到点![]() 时,若双曲线
时,若双曲线![]() 的图象恰好过点N,试求k的值;
的图象恰好过点N,试求k的值;
(3)△MNB与△OAB能否相似?若能试求出所有t的值,若不能请说明理由.
【答案】(1)见解析;(2)k=12;(3)能,t=6s或![]() s时,△BMN与△AOB相似.
s时,△BMN与△AOB相似.
【解析】
(1)用含t的式子表示OM,ON,可证得![]() ,即可解决问题;
,即可解决问题;
(2)根据M点坐标可求得运动时间,进而求得N点坐标,再利用待定系数法求解析式即可解决问题;
(3)分两种情形解决)①当点M与点A重合时,△BNM∽△BAO,此时求得t.②当OM=BM时,△MBN∽△BOA,此时点M在线段OB 的垂直平分线上,可求得此时t值
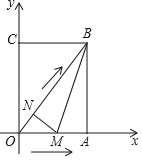
解:(1)证明:由题意:OA=6,AB=8,OB=10,OM=t,ON=0.6t,
∴![]() ,
,
∵∠MON=∠AOB,
∴△ONM∽△OAB.
(2)当OM=![]() 时,ON=5,
时,ON=5,
∴ON=NB,
∴N(3,4),
∵双曲线![]() 的图象恰好过点N,
的图象恰好过点N,
∴k=12.
(3)①当点M与点A重合时,△BNM∽△BAO,此时t=6s.
②当OM=BM时,∠MBN=∠AOB,∵∠OAB=∠MNB=90°,
∴△MBN∽△BOA,
此时点M在线段OB 的垂直平分线上,
由(2)可知,此时OM=![]() ,t=
,t=![]() s,
s,
综上所述,当t=6s或![]() s时,△BMN与△AOB相似.
s时,△BMN与△AOB相似.

练习册系列答案
相关题目