题目内容
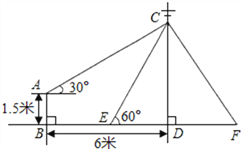
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角
∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长 (结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
【答案】5.7米
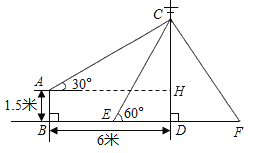
【解析】试题分析:过点A作AH⊥CD,垂足为H.在Rt△ACH中求出CH.在Rt△ECD中,再求出EC即可.
试题解析:解:过点A作AH⊥CD,垂足为H.由题意可知四边形ABDH为矩形,∠CAH=30°,∴AB=DH=1.5,BD=AH=6.在Rt△ACH中,tan∠CAH=![]() ,∴CH=AHtan∠CAH,∴CH=AHtan∠CAH=6tan30°=6×
,∴CH=AHtan∠CAH,∴CH=AHtan∠CAH=6tan30°=6×![]() =2
=2![]() .∵DH=1.5,∴CD=2
.∵DH=1.5,∴CD=2![]() +1.5.在Rt△CDE中,∵∠CED=60°,sin∠CED=
+1.5.在Rt△CDE中,∵∠CED=60°,sin∠CED=![]() ,∴CE=
,∴CE=![]() =4+
=4+![]() ≈5.7(米).
≈5.7(米).
答:拉线CE的长约为5.7米.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目