题目内容
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3
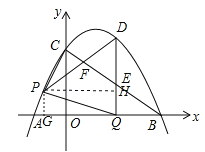
x+3![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x+3
x+3![]() ;(2)①P(
;(2)①P(![]() t﹣3,
t﹣3,![]() t),D(9﹣2t,﹣
t),D(9﹣2t,﹣![]() t2+
t2+![]() t),②
t),②![]() ;(3)t=3,F(
;(3)t=3,F(![]() ,
,![]() ).
).
【解析】试题分析:(1)先求出B、C两点的坐标,进而求出直线BC的函数表达式;
(2)①过点P作PG⊥x轴于点G ,由AO=3,BO=9,OC=![]() ,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=
,得到∠CAO=60°,∠APG=30°,从而有AP=t, AG=![]() ,PG=
,PG=![]() ,得到P的坐标.由OQ=
,得到P的坐标.由OQ=![]() ,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
,得到D的横坐标,由D在抛物线上,得到D的纵坐标;
②过点P作PG⊥x轴于点G,PH⊥QD于点H,得到四边形PGQH是矩形,从而有QD=2HQ=2PG,解关于t的方程即可;
(3)由中点坐标公式和F在直线BC上得到![]() ,解得t=3.把t=3代入得到F的坐标.
,解得t=3.把t=3代入得到F的坐标.
试题解析:(1)由y=0,得![]() ,解得:
,解得:![]() ,
,![]() ,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得
,∴点A的坐标为(-3,0),点B的坐标为(9,0).由x=0,得![]() ,∴点C的坐标为(0,
,∴点C的坐标为(0,![]() ).
).
设直线BC的函数表达式为:![]() ,∴
,∴![]() ,解得:
,解得: ,∴直线BC的函数表达式为:
,∴直线BC的函数表达式为:![]() ;
;
(2)①过点P作PG⊥x轴于点G .∵A(-3,0),B(9,0),C(0,![]() )∴AO=3,BO=9,OC=
)∴AO=3,BO=9,OC=![]() ,∴tan∠CAO=
,∴tan∠CAO=![]() ,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=
,∴∠CAO=60°,∴∠APG=30°,∵AP=t,∴AG=![]() ,PG=
,PG=![]() ,∴OG=3-
,∴OG=3-![]() ,∴P(
,∴P(![]() ,
,![]() ).∵OQ=
).∵OQ=![]() ,∴D的横坐标为
,∴D的横坐标为![]() ,∵D在抛物线
,∵D在抛物线![]() 上,∴D的纵坐标为
上,∴D的纵坐标为![]() =
=![]() ,∴D D(
,∴D D(![]() ,
,![]() ).
).
综上所述:P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() );
);
②过点P作PG⊥x轴于点G,PH⊥QD于点H.∵QD⊥x轴,∴四边形PGQH是矩形,∴HQ=PG.∵PQ=PD,PH⊥QD,∴QD=2HQ=2PG.
∵P、D两点的坐标分别为P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∴
),∴![]() =
=![]() ,解得:
,解得:![]() (舍去),
(舍去),![]() ,∴当PQ=PD时,t的值为
,∴当PQ=PD时,t的值为![]() .
.
(3)∵F为PD的中点,且P(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),由中点坐标公式得:F(
),由中点坐标公式得:F(![]() ,
,![]() ),∵F在直线BC上,∴
),∵F在直线BC上,∴![]() ,∴
,∴![]() ,解得:t=3.
,解得:t=3.
当t=3时,![]() =
=![]() ,
,![]() =
=![]() ,∴F(
,∴F(![]() ,
,![]() ).
).

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案