题目内容
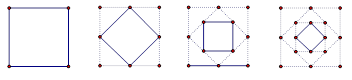
如图,在四边形ABCD中,对角线AC、BD相交于点O,直线MN经过点O,设锐角∠DOC=∠ ,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
(Ⅰ)当四边形ABCD是矩形时,如图1,请猜想A D’、B C’的数量关系以及∠APB与∠α的大小关系;
(Ⅱ)当四边形ABCD是平行四边形时,如图2,(1)中的结论还成立吗?
(Ⅲ)当四边形ABCD是等腰梯形时,如图3,∠APB与∠α有怎样的数量关系?请证明.

 ,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.(Ⅰ)当四边形ABCD是矩形时,如图1,请猜想A D’、B C’的数量关系以及∠APB与∠α的大小关系;
(Ⅱ)当四边形ABCD是平行四边形时,如图2,(1)中的结论还成立吗?
(Ⅲ)当四边形ABCD是等腰梯形时,如图3,∠APB与∠α有怎样的数量关系?请证明.

(Ⅰ)A D’=B C’,∠APB=∠α.
(Ⅱ) A D’=B C’仍然成立,∠APB=∠α不一定成立.
(Ⅲ)∠APB=180°-∠α.
证明:如图3,设OC’,PD’交于点E.
∵ 将△DOC以直线MN为对称轴翻折得到△D’OC’,
∴ △DOC≌△D’OC’,
∴ OD=OD’, OC=OC’,∠DOC=∠D’OC’.
∵ 四边形ABCD是等腰梯形,
∴ AC=BD,AB="CD," ∠ABC= ∠DCB.
∵ BC=CB,
∴ △ABC≌△DCB.
∴ ∠DBC=∠ACB.
∴ OB=OC,OA=OD.
∵ ∠AOB= ∠COD=∠C’O D’,
∴ ∠BOC’ = ∠D’O A.
∵ OD’=OA,OC’=OB,
∴ △D’OC’≌△AOB,
∴ ∠OD’C’= ∠OAB .
∵ OD’=OA,OC’=OB,∠BOC’ = ∠D’O A,
∴ ∠OD’A = ∠OAD’=∠OBC’=∠OC’ B.
∵ ∠C’EP= ∠D’EO,
∴ ∠C’PE= ∠C’OD’=∠COD=∠α.
∵∠C’PE+∠APB=180°,
∴∠APB=180°-∠α.
(Ⅱ) A D’=B C’仍然成立,∠APB=∠α不一定成立.
(Ⅲ)∠APB=180°-∠α.
证明:如图3,设OC’,PD’交于点E.
∵ 将△DOC以直线MN为对称轴翻折得到△D’OC’,
∴ △DOC≌△D’OC’,
∴ OD=OD’, OC=OC’,∠DOC=∠D’OC’.
∵ 四边形ABCD是等腰梯形,
∴ AC=BD,AB="CD," ∠ABC= ∠DCB.
∵ BC=CB,
∴ △ABC≌△DCB.
∴ ∠DBC=∠ACB.
∴ OB=OC,OA=OD.
∵ ∠AOB= ∠COD=∠C’O D’,
∴ ∠BOC’ = ∠D’O A.
∵ OD’=OA,OC’=OB,
∴ △D’OC’≌△AOB,
∴ ∠OD’C’= ∠OAB .
∵ OD’=OA,OC’=OB,∠BOC’ = ∠D’O A,
∴ ∠OD’A = ∠OAD’=∠OBC’=∠OC’ B.
∵ ∠C’EP= ∠D’EO,
∴ ∠C’PE= ∠C’OD’=∠COD=∠α.
∵∠C’PE+∠APB=180°,
∴∠APB=180°-∠α.
(1)根据矩形的性质及角之间的关系证明△BOD′≌△AOC′,得出对应边对应角相等,推理即可得出结论;
(2)先进行假设,然后根据平行四边形的性质及相似三角形比例关系即可得出答案;
(3)易证△BOD′≌△C′OA,则AC′=BD′,∠OBD′=∠OC′A≠∠OAC′,从而得出∠AMB≠α.
(2)先进行假设,然后根据平行四边形的性质及相似三角形比例关系即可得出答案;
(3)易证△BOD′≌△C′OA,则AC′=BD′,∠OBD′=∠OC′A≠∠OAC′,从而得出∠AMB≠α.

练习册系列答案
相关题目