题目内容
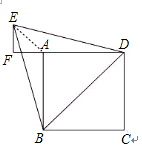
如图,已知四边形ABCD是边长为2的正方形,以对角线BD为边作正三角形BDE,过E作DA 的延长线的垂线EF,垂足为F。

(1)找出图中与EF相等的线段,并证明你的结论;
(2)求AF的长。

(1)找出图中与EF相等的线段,并证明你的结论;
(2)求AF的长。
(1)AF=EF;
理由如下:连接AE,
∵△DBE是正三角形,
∴EB=ED.
∵AD=AB,AE=AE,
∴△ABE≌△ADE.
∴∠BEA=∠DEA=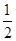 ×60°=30°.
×60°=30°.
∵∠EDA=∠EDB-∠ADB=60°-45°=15°,
∴∠EAF=∠AED+∠ADE=45°.
∵EF⊥AD,
∴△EFA是等腰直角三角形.
∴EF=AF.
(2)设AF=x,
∵AD=2,BD=2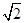 =ED,FD=2+x,
=ED,FD=2+x,
在Rt△EFD中,
由勾股定理得EF2+FD2=ED2
即x2+(2+x)2=(2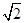 )2
)2
∴x=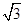 -1(x=-
-1(x=-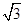 -1舍去),∴AF=
-1舍去),∴AF=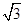 -1.
-1.
理由如下:连接AE,
∵△DBE是正三角形,
∴EB=ED.
∵AD=AB,AE=AE,
∴△ABE≌△ADE.
∴∠BEA=∠DEA=
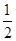 ×60°=30°.
×60°=30°.∵∠EDA=∠EDB-∠ADB=60°-45°=15°,
∴∠EAF=∠AED+∠ADE=45°.
∵EF⊥AD,
∴△EFA是等腰直角三角形.
∴EF=AF.
(2)设AF=x,
∵AD=2,BD=2
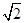 =ED,FD=2+x,
=ED,FD=2+x,在Rt△EFD中,
由勾股定理得EF2+FD2=ED2
即x2+(2+x)2=(2
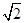 )2
)2∴x=
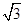 -1(x=-
-1(x=-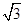 -1舍去),∴AF=
-1舍去),∴AF=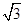 -1.
-1.
(1)连接AE,首先证明△ABE≌△ADE得到∠BEA=30°,再根据题意∠EAF=∠AED+∠ADE=45°,又知EF⊥AD,故可得AF=EF,
(2)设AF=x,由勾股定理得EF2+FD2=ED2,列出等量关系式,解得x.
(2)设AF=x,由勾股定理得EF2+FD2=ED2,列出等量关系式,解得x.

练习册系列答案
相关题目

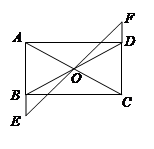





 ,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
,将△DOC以直线MN为对称轴翻折得到△D’OC’,直线A D’、B C’相交于点P.
