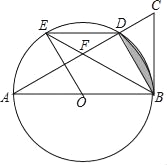
题目内容
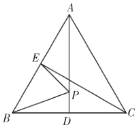
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是⊙O的切线.
(2)若PB=3,DB=4,求DE的长.
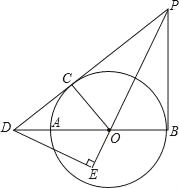
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由已知角相等,及对顶角相等得到三角形DOE与三角形POB相似,利用相似三角形对应角相等得到∠OBP为直角,即可得证;
(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB,由PD-PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=8-r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,然后通过相似三角形的性质即可得到结论.
(1)∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2)解:在Rt△PBD中,PB=3,DB=4,
根据勾股定理得:PD=![]() =5,
=5,
∵PD与PB都为圆的切线,
∴PC=PB=3,
∴DC=PD﹣PC=5﹣3=2,
在Rt△CDO中,设OC=r,则有DO=4﹣r,
根据勾股定理得:(4﹣r)2=r2+22,
解得:r=![]() ,
,
∴OP=![]() ,
,
∵∠E=∠PBO,∠DPE=∠OPB,
∴△DEP∽△OBP,
∴![]() ,
,
∴DE=![]() .
.

【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.

【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
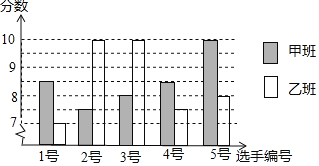
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.