Question

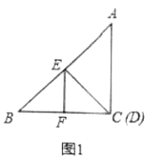
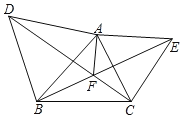
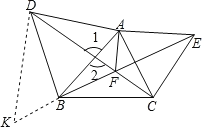
【题目】如图，分别以△ABC的边AB，AC向外作两个等边三角形△ABD，△ACE．连接BE、CD交点F，连接AF．

（1）求证：△ACD≌△AEB；

（2）求证：AF+BF+CF=CD．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）根据等边三角形的性质得到AD＝AB，AC＝AE，∠BAD＝∠CAB＝60，根据全等三角形的判定定理即可得到结论；

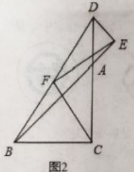
（2）如图，延长FB至K，使FK＝DF，连DK，根据等边三角形的性质和全等三角形的判定和性质定理即可得到结论．

（1）∵△ABD和△ACE为等边三角形，

∴AD=AB，AC=AE，∠BAD=∠CAB=60°，

∴∠DAC=∠BAE=60°+∠BAC．

在△ACD和△AEB中，

∵，

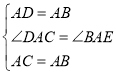∴△ACD≌△AEB(SAS)；

（2）由（1）知∠CDA=∠EBA，

如图∠1=∠2，

∴180°﹣∠CDA﹣∠1=180°﹣∠EBA﹣∠2，

∴∠DAB=∠DFB=60°，

如图，延长FB至K，使FK=DF，连DK，

∴△DFK为等边三角形，

∴DK=DF，

∴△DBK≌△DAF(SAS)，

∴BK=AF，

∴DF=DK，FK=BK+BF，

∴DF=AF+BF，

又∵CD=DF+CF，

∴CD=AF+BF+CF．