Question

如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线.

（1）矩形有    条面积等分线；
（2）如图①，在矩形中剪去一个小正方形，这个图形有    条面积等分线，请画出这个图形的一条面积等分线，并说明理由；
（3）如图②，在矩形中剪去两个小正方形，请画出这个图形的一条面积等分线，并说明理由．

Answer 1

（1）  无数    ；  （2）  无数   ；（3）（答案不唯一）

试题分析：（1）对于平行四边形应该有无数条，只要过两条对角线的交点的直线都可以把平行四边形的面积分成2个相等的部分；
（2）无数
如图①为其中一条面积等分线(答案不唯一).  2分

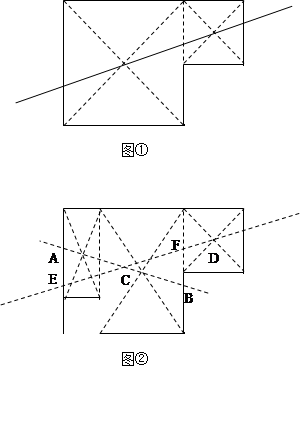
理由：由矩形的中心对称性可得.             2分
（3）如图②为其中一条面积等分线(答案不唯一).  2分
由矩形的中心对称性可得直线AB,
取线段AB中点,得直线CD.         
由△AEC≌△BFC,易证直线CD为该图形的
一条面积等分线.                 2分
点评：此题可以归类为阅读型题，主要通过给出学生没有接触过的定义，让学生把这些定理规定运用到解答此题中，解决此类题，关键是理解题目给出的定义，根据定义去解题。