题目内容
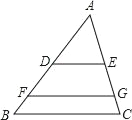
【题目】如图，在△ABC中，点D，F在AB上，点E，G在AC上，DE∥FG∥BC，且S△ADE=S四边形DFGE=S四边形FBCG
（1）求DE：FG：BC的值；
（2）若AB=10，AC=15，BC=12，求四边形DFGE的周长．
【答案】（1）1：
：
（2）
【解析】
（1）由DE∥FG∥BC知△ADE∽△AFG∽△ABC，根据题意可得
，
，利用相似三角形的性质即可得出答案；
（2）由
、BC=12知FG=4
，由
、FG=4知DE=4，从而得DF=
，同理求得GE=5-5，根据周长公式即可得出答案．
（1）∵S△ADE=S梯形DFGE=S梯形FBCG，
∵DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∴，，
由于相似三角形的面积比等于对应边长的平方比，
∴DE：FG：BC=1：
．
（2）∵，BC=12，
∴FG=
，
∵，FG=4，
∴DE=
，
∴DF=，
同理可得GE=5﹣5，
∴四边形DFGE的周长为DF+FG+GE+DE
=+4+5﹣5+4=．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
