题目内容
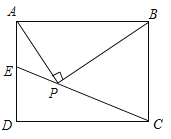
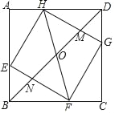
【题目】在边长为3的正方形ABCD中，点E、F、G、H分别在AB、BC、CD、DA边上，且满足EB=FC=GD=HA=1，BD分别与HG、HF、EF相交于M、O、N给出以下结论：
①HO=OF；②OF2=ONOB；③HM=2MG；④S△HOM=
，其中正确的个数有（ ）
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
根据正方形的性质、全等三角形的判定和性质、角平分线的性质定理一一判断即可．
作MP⊥AD于P，MQ⊥CD于Q．连接OG．
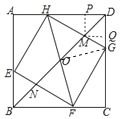
∵四边形ABCD是正方形，∴AD∥BC，AD=BC．
∵AH=CF，∴DH=BF，∠ODH=∠OBF．
∵∠DOH=∠BOF，∴△DOH≌△BOF，∴OH=OF，故①正确．
∵∠FON=∠FOB，∠OFN=∠OBF=45°，∴△OFN∽△OBF，∴OF2=ONOB，故②正确．
∵∠MDH=∠MDG，MP⊥AD于P，MQ⊥CD于Q，∴MP=MQ．
∵
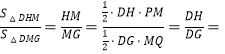2，∴HM=2MG，故③正确．
∵正方形EFGH的面积=5，∴S△OHG的面积
，∴S△OMH
，故④正确．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
