Question

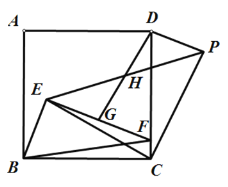
【题目】如图，E为正方形ABCD内一点，点F在CD边上，且∠BEF＝90°，EF＝2BE．点G为EF的中点，点H为DG的中点，连接EH并延长到点P，使得PH＝EH，连接DP．

（1）依题意补全图形；

（2）求证：DP＝BE；

（3）连接EC，CP，猜想线段EC和CP的数量关系并证明．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）详见解析

【解析】

（1）根据题意可以画出完整的图形；
（2）由EF＝2BE，点G为EF的中点可知，要证明DP＝BE，只要证明DP=EG即可，要证明DP=EG，只要证明ΔPDH≌ΔEGH即可，然后根据题目中的条件和全等三角形的判定即可证明结论成立；
（3）首先写出线段EC和CP的数量关系，然后利用全等三角形的判定和性质即可证明结论成立．

解：（1）依题意补全图形如下：

（2）∵点H为线段DG的中点，

∴DH＝GH．

在ΔPDH和ΔEGH中，

∵EH=PH，∠EHG=∠PHD，

∴ΔPDH≌ΔEGH（SAS）．

∴DP＝EG．

∵G为EF的中点，

∴EF＝2EG．

∵EF＝2EB，

∴BE＝EG＝DP．

（3）猜想：EC=CP．

由（2）可知ΔPDH≌ΔEGH．

∴∠HEG=∠HPD．

∴DP∥EF．

∴∠PDC=∠DFE．

又∵∠BEF=∠BCD=90°，

∴∠EBC+∠EFC=180°．

又∵∠DFE+∠EFC=180°，

∴∠EBC=∠DFE=∠PDC．

∵BC=DC，DP=BE，

∴ΔEBC≌ΔPDC（SAS）．

∴EC=PC．

故答案为：（1）详见解析；（2）详见解析；（3）详见解析．