题目内容
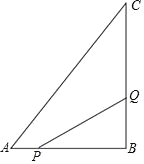
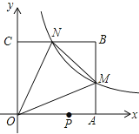
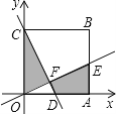
【题目】如图,在直角坐标系中,正方形OABC顶点B的坐标为(6,6),直线CD交直线OA于点D,直线OE交线段AB于点E,且CD⊥OE,垂足为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为______.
,则△OFC的周长为______.
【答案】6+2![]()
【解析】
证明△COD≌△OAE,推理出△OCF面积=四边形FDAE面积=12÷2=6,设OF=x,FC=y,则xy=12,x2+y2=36,所以(x+y)2=x2+y2+2xy=60,从而可得x+y的值,则△OFC周长可求.
∵正方形OABC顶点B的坐标为(6,6),
∴正方形的面积为36.
所以阴影部分面积为36×![]() =12.
=12.
∵四边形AOCB是正方形,
∴∠AOC=90°,即∠COE+∠AOE=90°,
又∵CD⊥OE,
∴∠CFO=90°
∴∠OCF+∠COF=90°,
∴∠OCD=∠AOE
在△COD和△OAE中

∴△COD≌△OAE(AAS).
∴△COD面积=△OAE面积.
∴△OCF面积=四边形FDAE面积=12÷2=6.
设OF=x,FC=y,
则xy=12,x2+y2=36,
所以(x+y)2=x2+y2+2xy=60.
所以x+y=2![]() .
.
所以△OFC的周长为6+2![]() .
.
故答案为6+2![]() .
.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目