题目内容
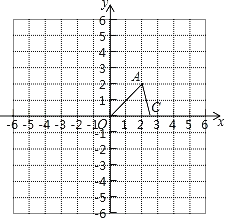
【题目】如图在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上点,点
是抛物线上点,点![]() 为射线
为射线![]() 上点(不含
上点(不含![]() 两点),且
两点),且![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 及抛物线解析式;
及抛物线解析式;
(2)如图,过点![]() 作
作![]() 轴,且与抛物线交于
轴,且与抛物线交于![]() 两点(
两点(![]() 位于
位于![]() 左边),若
左边),若![]() ,点
,点![]() 为直线
为直线![]() 上方的抛物线上点,求
上方的抛物线上点,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标;
的坐标;
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)抛物线表达式中有两个未知数,所以只需代入两个点的坐标即可求出表达式,直线![]() 为正比例函数,只需一个点即可求出表达式;
为正比例函数,只需一个点即可求出表达式;
解:(1)设直线![]() 表达式为
表达式为![]() ,
,
把![]() 代入表达式得:
代入表达式得:
![]() ,
,
![]() 直线
直线![]() 表达式为:
表达式为:![]() ;
;
把点![]() ,点
,点![]() 代入二次函数
代入二次函数![]() 中,得:
中,得:
![]() ,
,
解得: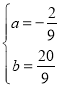 ,
,
![]() 二次函数表达式为:
二次函数表达式为:![]() ;
;
(2)根据题意:
设![]() ,
,
把点C代入(1)中二次函数表达式得:
![]() ,
,
得到:![]() ,
,
![]() ,
,
![]() ,
,
联立①②得:![]() ,
,
![]() ,如图所示,
,如图所示,
分别过点B,点Q,点C作![]() ,
,
则![]() ,
,
设![]() ,代入上式整理得:
,代入上式整理得:![]() ,
,
![]() 时面积最大,
时面积最大,
此时![]() ;
;

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
【题目】如图,扇形OAB的圆心角为90°,点C、D是![]() 的三等分点,半径OC、OD分别与弦AB交于点E、F,下列说法错误的是( )
的三等分点,半径OC、OD分别与弦AB交于点E、F,下列说法错误的是( )
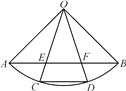
A.AE=EF=FBB.AC=CD=DB
C.EC=FDD.∠DFB=75°
【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。