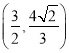题目内容
【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润
(元)的最大值及相应的值。
【答案】（1）
；
；；（2）当
时,总利润
最大值为3198元.
【解析】
（1）根据题意列代数式即可；
（2）根据每天甲、丙两种产品的产量相等得到m与x之间的关系式，用x表示总利润利用二次函数性质讨论最值．
（1）由已知，每天安排x人生产乙产品时，生产甲产品的有（65x）人，共生产甲产品2（65x）1302x件．在乙每件120元获利的基础上，增加x人，利润减少2x元每件，则乙产品的每件利润为1202（x5）＝1302x．
故答案为：65x；1302x；1302x；
（2）设生产甲产品m人
W＝x（1302x）＋15×2m＋30（65xm）
＝2（x25）2＋3200
∵2m＝65xm
∴m＝
∵x、m都是非负整数
∴取x＝26时，m＝13，65xm＝26
即当x＝26时，W最大值＝3198
答：安排26人生产乙产品时，可获得的最大利润为3198元．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】下表是某班同学随机投掷一枚硬币的试验结果（ ）
抛掷次数n | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数m | 22 | 52 | 71 | 95 | 116 | 138 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.47 | 0.48 | 0.46 | 0.46 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断：
①表中没有出现“正面向上”的概率是0.5的情况，所以不能估计“正面向上”的概率是0.5；
②这些次试验投掷次数的最大值500，此时“正面向上”的频率是0.48，所以“正面向上”的概率是0.48；
③投掷硬币“正面向上”的概率应该是确定的，但是大量重复试验反映的规律并非在每一次试验中都发生；
其中合理的是（ ）
A. ①②B. ①③C. ③D. ②③
