题目内容
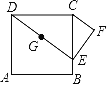
【题目】正方形ABCD,边长为4,E是边BC上的一动点,连DE,取DE中点G,将GE绕E顺时针旋转90°到EF,连接CF,当CE为_____时,CF取得最小值.
【答案】![]()
【解析】
作GM⊥BC于M,FN⊥BC于N,证出GM是△CDE是中位线,得出CM=EM,GM=![]()
CD=2,由旋转的性质得出EF=EG,∠GEF=90°,证明△GEM≌△EFN(AAS),得出GM=EN=2,EM=FN,设CE=x,则CM=EM=FN=![]() x,在Rt△CFN中,由勾股定理得出CF2=CN2+FN2=
x,在Rt△CFN中,由勾股定理得出CF2=CN2+FN2=![]() ,由二次函数的性质即可得出答案.
,由二次函数的性质即可得出答案.
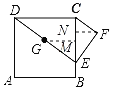
作GM⊥BC于M,FN⊥BC于N,如图所示:
则GM∥CD,
∵四边形ABCD是正方形,∴BC=CD=4,
∵G是DE的中点,
∴GM是△CDE是中位线,
∴CM=EM,GM=![]() CD=2,
CD=2,
由旋转的性质得:EF=EG,∠GEF=90°,
即∠GEM+∠FEN=90°,
∵∠GEM+∠EGM=90°,
∴∠EGM=∠FEN,
在△GEM和△EFN中,
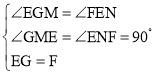 ,
,
∴△GEM≌△EFN(AAS),
∴GM=EN=2,EM=FN,
设CE=x,则CM=EM=FN=![]() x,
x,
在Rt△CFN中,由勾股定理得:CF2=CN2+FN2=(x﹣2)2+(![]() x)2=
x)2=![]() x2﹣4x+4=
x2﹣4x+4=![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,CF的最小值=
时,CF的最小值=![]() =
=![]() ;
;
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目