题目内容
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)由平行四边形的性质和角平分线易证∠BAE=∠BEA,根据等腰三角形的性质可得AB=BE;(2)易证△ABE是等边三角形,根据等边三角形的性质可得AE=AB=4,AF=EF=2,由勾股定理求出BF,再由AAS证明△ADF≌△ECF,即△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=![]() AEBF,即可得出结果.
AEBF,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF=![]() ,
,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
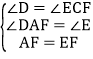 ,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=![]() AEBF=
AEBF=![]() ×4×2
×4×2![]() =4
=4![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目