题目内容
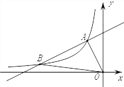
【题目】如图,点A、B在双曲线y=![]() (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=![]() (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.

【答案】![]()
【解析】
如图,过A点作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,设A(a,﹣![]() ),C(b,
),C(b,![]() ),根据△ABF≌△COE可得B(a+b,﹣
),根据△ABF≌△COE可得B(a+b,﹣![]() ),即(a+b)(﹣
),即(a+b)(﹣![]() )=﹣3,设
)=﹣3,设![]() =m,则可化方程为3m﹣
=m,则可化方程为3m﹣![]() =2,求得
=2,求得![]() =
=![]() ,
,![]() ,然后根据□OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
,然后根据□OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
解:如图,连接AC,过A点作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,
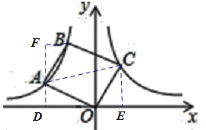
易证△ABF≌△COE,设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
∵B点在在双曲线y=![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
设![]() =m,则可化方程为3m﹣
=m,则可化方程为3m﹣![]() =2,
=2,
解得m=![]() ,或m=
,或m=![]() (舍去),
(舍去),
∴![]() =
=![]() ,
,![]() ,
,
∴S□OABC=2×S△OAC
=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×∣﹣3∣﹣
×∣﹣3∣﹣![]() ×2]
×2]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目