题目内容
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

【答案】2![]() +2
+2
【解析】如图所示,
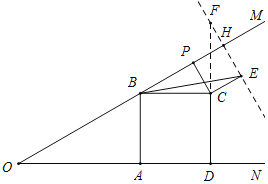
将BC绕着点C顺时针旋转90°得FC,作直线FE交OM于H,则∠BCF=90°,BC=FC,
∵将CP绕点C按顺时针方向旋转90°得CE,
∴∠PCE=90°,PC=EC,
∴∠BCP=∠FCE,
在△BCP和△FCE中,
BC=FC,∠BCP=∠FCE,PC=EC,
∴△BCP≌△FCE(SAS),
∴∠CBP=∠CFE,
又∵∠BCF=90°,
∴∠BHF=90°,
∴点E在直线FH上,即点E的轨迹为直线FH,
∵BH⊥EF,
∴当点E与点H重合时,BE=BH最短,
∵当CP⊥OM时,Rt△BCP中,∠CBP=30°,
∴CP=![]() BC=2,BP=
BC=2,BP=![]() CP=2
CP=2![]() ,
,
又∵∠PCE=∠CPH=∠PHE=90°,CP=CE,
∴正方形CPHE中,PH=CP=2,
∴BH=BH+PH=2![]() +2,
+2,
即BE的最小值为2![]() +2,
+2,
故答案为:2![]() +2.
+2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
