题目内容
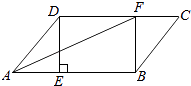
【题目】如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )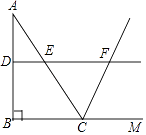
A.6
B.7
C.8
D.9
【答案】D
【解析】解:∵∠ABC=90°,AB=12,BC=5,
∴AC= ![]() =13,
=13,
∵DE是△ABC的中位线,
∴DE= ![]() BC=2.5,DE∥BC,EC=
BC=2.5,DE∥BC,EC= ![]() AC=6.5,
AC=6.5,
∵CF是△ABC的外角∠ACM的平分线,
∴∠ECF=∠MCF,
∵DE∥BC,
∴∠EFC=∠MCF,
∴∠ECF=∠EFC,
∴EF=EC=6.5,
∴DF=DE+EF=9,
所以答案是:D.
【考点精析】根据题目的已知条件,利用三角形的外角和三角形中位线定理的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 ![]() 与方差s2:
与方差s2:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2(cm2) | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁